The God of the Gap
There lies, at the heart of reality, a fundamental paradox: The amount of information necessary to describe any complex system exceeds the information-storage capacity of such system. If you understand the necessary consequences of this, please feel free to continue reading so you can acquire a method for explaining this to the common man. For everyone else: I have just conclusively and irrefutably demonstrated the existence of God. Let me elaborate.
For a number of reasons, we will be using the simplest possible set of complex systems. We will be using eight systems — seven complex and one simple (to demonstrate the difference). First, our simple system: Z. In system Z, we have one entity and zero connections, yielding a total of one point. An entity is simply a thing in our system; in all of our hypothetical systems, our entities are binary, which is to say that they have only two possible states, which we will call on and off, for the sake of simplicity (but any other binary designation would do, so, on and off, left and right, et cetera). A connection is a relationship between two entities1; in our hypothetical systems, we will call these connections up or down (as they are also binary, to keep the complexity to a bare minimum). Lastly, points are simply entities or connections — it is a term to encompass both.
System Z is simple and so is distinguishable from our other systems; in fact, it is included only to demonstrate what is meant by “simple” and “complex” in this matter.
Our first complex system is A, which has two entities, one connection, and, thus, a total of three points. Now, this system may seem ‘simple’, but it is complex in the sense in which we are employing the term. Each entity can theoretically store one bit of data — on or off —, which means the system has an information-storage capacity of two bits. Surely the problem is already obvious: The system requires three bits to describe — one each for the entities and one for the connection. Already with the simplest possible complex system, we see that the information necessary to describe the system exceeds the ability of the system to store information. This problem does not get better as complexity increases.
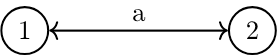
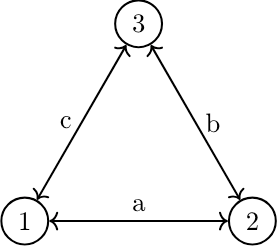
Our second system is B, which has three entities, three connections, and, thus, a total of six points. This system can theoretically store three bits of information (one per entity), but it takes six bits of information to describe it. System A was ‘short’ one bit, but system B is short three bits. Our problem is accelerating.
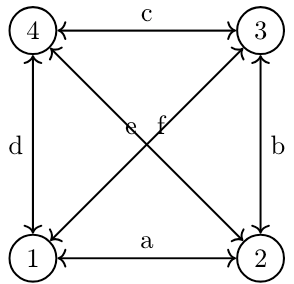
Our third system is C, which has four entities, six connections, and, thus, a total of ten points. This system can theoretically store four bits of information (one per entity), but it takes ten bits of information to describe it. System B was short three bits, but system C is short six bits. Our problem is accelerating.
Our fourth system is D, which has five entities, ten connections, and, thus, a total of fifteen points. This system can theoretically store five bits of information (one per entity), but it takes fifteen bits of information to describe it. System C was short six bits, but system D is short ten bits. Our problem is accelerating.
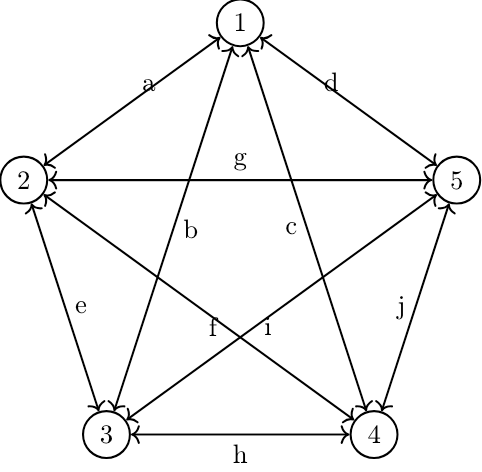
[[I will not be providing diagrams for the remaining example systems, as the size and complexity of the diagrams quickly gets out of hand. The four provided diagrams should be sufficient to drive home the point visually. Also, n.b., the diagrams are merely a visualization aid.]]
Our fifth system is E, which has six entities, fifteen connections, and, thus, a total of twenty-one points. This system can theoretically store six bits of information (one per entity), but it takes twenty-one bits of information to describe it. System D was short ten bits, but system E is short fifteen bits. Our problem is accelerating.
Our sixth system is F, which has seven entities, twenty-one connections, and, thus, a total of twenty-eight points. This system can theoretically store seven bits of information (one per entity), but it takes twenty-eight bits of information to describe it. System E was short fifteen bits, but system F is short twenty-one bits. Our problem is accelerating.
Our seventh, and final, system is G, which has eight entities, twenty-eight connections, and, thus, a total of thirty-six points. This system can theoretically store eight bits of information (one per entity), but it will take thirty-six bits of information to describe it. System F was short twenty-one bits, but system G is short twenty-eight bits. Both the existence and the exponential nature of the problem is assuredly clear at this point.
Some will undoubtedly have discerned the pattern already, but here is the table:
| System | Entities | Connections | Bits | Deficit | Calculation |
|---|---|---|---|---|---|
| A | 2 | 1 | 3 | -1 | (2² + 2)/2 |
| B | 3 | 3 | 6 | -3 | (3² + 3)/2 |
| C | 4 | 6 | 10 | -6 | (4² + 4)/2 |
| D | 5 | 10 | 15 | -10 | (5² + 5)/2 |
| E | 6 | 15 | 21 | -15 | (6² + 6)/2 |
| F | 7 | 21 | 28 | -21 | (7² + 7)/2 |
| G | 8 | 28 | 36 | -28 | (8² + 8)/2 |
As can be clearly seen in the table, each additional entity adds n-1 (where n is the number of entities in the ‘new’ system) to the information deficit (e.g., the second entity added required one more bit to describe than the system could provide and the fourth entity added required three more bits to describe than the system could provide); this pattern continues indefinitely. Here is the overall formula to calculate the total number of bits to describe a given system (n = number of entities):
$${(n^{2}+n})/2$$
It would be trivial to make a chart demonstrating this deficit — or gap — to thousands, millions, or even billions of total entities. There are somewhere in the vicinity of \( 10^{80} \) atoms in the Universe. Each atom is a complex system, and they form additional complex systems. We are ignoring the Gestalt problem with our hypothetical systems, but it is important to remember that it cannot be ignored when dealing with the information paradox with regard to the real world.
The problem is, in fact, insurmountable. It is not merely theoretically irresolvable — it is literally impossible to resolve, at least naturalistically. Any system complex enough to describe another complex system will be unable to describe itself. This continues to infinity, but there is our solution: Infinity.
The only entity with sufficient capacity to describe all complex systems is itself not complex, but simple; further, such Entity is necessarily infinite. Such Entity is, in fact, the Infinite. Such Entity is God.
The information paradox is resolvable only by resorting to the infinitude of God. Any other proposed ‘solution’ will only exacerbate the problem — creating more complexity that is even less describable than the lesser complexity it endeavors to describe. In His absolute divine simplicity, God requires no information outside Himself to describe — He is system Z. In His infinitude, God possesses ‘storage capacity’ far in excess of what would be necessary to describe even the most complex system (i.e., the Universe), for, of course, He created them all. Somewhat more formally:
- There can exist only one (absolute) Infinite.
- Any complex system requires more information to describe it than it can possibly contain.
- Complex systems exist.
- The Infinite exists. {3+2}
- God exists. {4+1}
In short: The existence of any complex system necessarily entails the existence of God, and complex systems very clearly exist. QED.
-
For the sake of simplicity, we are ignoring the problem presented by the fact that the Gestalt, being greater than the mere sum of the parts that comprise it, would, in fact, require even more information-storage capacity to fully describe. ↩︎